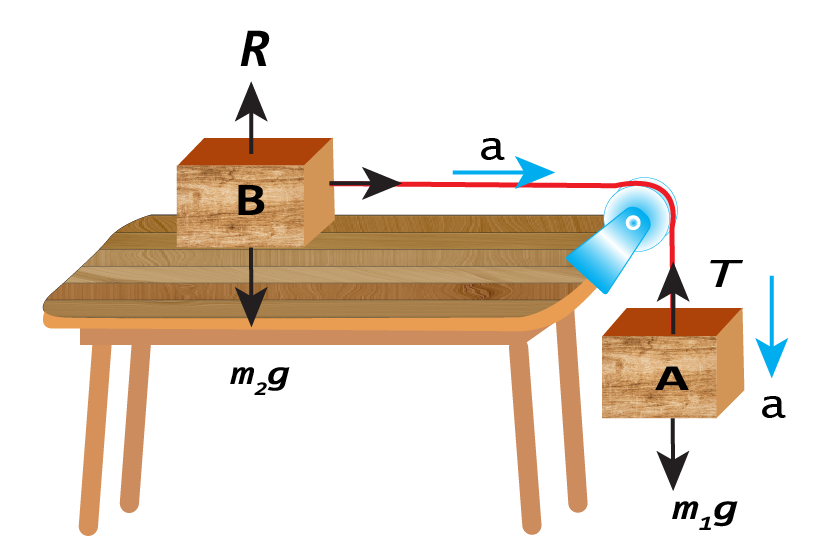
 Consider two bodies A and B of masses m1 and m2 respectively attached to the ends of an inextensible string as shown in figure.
Let the body A moves downwards with an acceleration \(a\). Since the string is inextensible, therefore, body B also moves over the horizontal surface with the same acceleration \(a\). As the pulley is frictionless, so tension T will be the same throughout the string.
Consider two bodies A and B of masses m1 and m2 respectively attached to the ends of an inextensible string as shown in figure.
Let the body A moves downwards with an acceleration \(a\). Since the string is inextensible, therefore, body B also moves over the horizontal surface with the same acceleration \(a\). As the pulley is frictionless, so tension T will be the same throughout the string.
Consider Body A:
Since body A moves downwards, therefore, its weight m1g is greater than the tension T in the string.
$$ Net \; force \; acting \; on \; body \; A = m_{1}g-T $$ $$ m_{1}a= m_{1}g – T \; \; \; \cdot \cdot \cdot (1)$$According to Newton's second law of motion, The forces acting on body B are:
- Weight m2g of the body B acting downward.
- Reaction R of the horizontal surface acting on body B in the upwards direction.
- Tension T in the string pulling the body B horizontally over the smooth surface.
As body B has no vertical motion, hence resultant of vertical forces (m2g and R) must be zero. Thus, the net force acting on body B is T.
According to Newton's second law of motion; $$T = m_{2}a \; \; \; \cdot \cdot \cdot (2)$$
we get acceleration by adding Eqs. 1 and 2 and putting value of T in eq 1
$$ m_{1}a = m_{1}g – m_{2}a $$ $$ (m_{1} + m_{2})a = m_{1}g $$ $$ a = \frac{m_{1}}{m_{1}+ m_{2}} g \; \; \; \cdot \cdot \cdot (3)$$ Putting the value of a in equations 2 to get tension T as $$ T= \frac{m_{1} m_{2}}{m_{1}+ m_{2}} g \; \; \; \cdot \cdot \cdot (4)$$