Equilibrium:
CONDITIONS FOR EQUILIBRIUM
In the above examples, we see that a body at rest or in uniform motion is in equilibrium if the resultant force acting on it is zero. For a body in equilibrium, it must satisfy certain conditions. There are two conditions for a body to be in equilibrium.
FIRST CONDITION FOR EQUILIBRIUM
First condition for equilibrium can be stated as:
“if the resultant of all the forces acting on a body is zero, the body is in equilibrium”
Let n number of forces F1, F2, F3, ...........,Fn are acting on a body such that $$ F_{1}+F_{2}+F_{3}+ \cdot \cdot \cdot \cdot + F_{n} = 0 $$ $$\sum F_{n} = 0 \; \; \; \; \cdot \cdot \cdot \cdot (1) $$ The symbol is a Greek letter Σ called sigma is used for summation. Equation 1 is called the first condition for equilibrium.
The first condition for equilibrium can also be stated in terms of x and y-components of the forces acting on the body as: $$ F_{1x}+F_{2x}+F_{3x}+\cdot \cdot \cdot \cdot + F_{nx} = 0 \; \; \; \; \cdot \cdot \cdot \cdot (2) $$ $$F_{1y}+F_{2y}+F_{3y}+\cdot \cdot \cdot \cdot + F_{ny} = 0 \; \; \; \; \cdot \cdot \cdot \cdot (3) $$ $$ \sum F_{x} =0 $$ $$ \sum F_{y} =0 $$ A book lying on a table or a picture hanging on a wall, are at rest and thus satisfy first condition for equilibrium. A paratrooper coming down with terminal velocity (constant velocity) also satisfies first condition for equilibrium and is thus in equilibrium.
SECOND CONDITION FOR EQUILIBRIUM
First condition for equilibrium does not ensure that a body is in equilibrium. This is clear from the following example.
Consider a body pulled by the forces F1 and F2 as shown in figure 1 (a). The two forces are equal but opposite to each other.
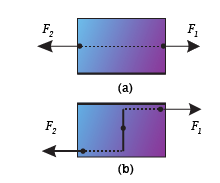 Both are acting along the same line, hence their resultant will be zero. According to the first condition, the body will be in equilibrium.
Both are acting along the same line, hence their resultant will be zero. According to the first condition, the body will be in equilibrium.
Now shift the location of the forces as shown in figure 1 (b). In this situation, the body is not in equilibrium although the first condition for equilibrium is still satisfied. It is because the body has the tendency to rotate.
This situation demands another condition for equilibrium in addition to the first condition for equilibrium. This is called second condition for equilibrium. According to this
A body satisfies second condition for equilibrium when the resultant torque acting on it is zero.
Mathematically,
$$ \sum \tau = 0 $$