Resistance:
The property of a substance which offers opposition to the flow of current through it is called its
resistance.
This opposition comes from the collisions of moving electrons with atoms of the substance.
Unit of Resistance: ohm (Ω)
The SI unit of resistance R is ohm.
If we put V = 1 V, and I = 1 A, the value of R will be 1 Ω.
Thus When a potential difference of one volt is applied across the ends of a conductor and one ampere of current passes through it, then its resistance will be one ohm.
Ohm’s law
If V is the potential difference across the two ends of any conductor, then current I will flow through it. The value of the current changes with the changes in potential difference and
is explained by Ohm's law, stated as:
The amount of current passing through a conductor is directly proportional to the potential difference applied across its ends, provided the temperature and the physical state of the
conductor does not change.
$$ V \propto R $$
$$ or \;\;\;\; V = IR $$
where R is the constant of proportionality and is the resistance of the conductors. Its SI unit is ohm and is denoted by a symbol Ω.
If a graph is plotted between the current I and the potential difference V, a straight line will be obtained.
Parallel Combination
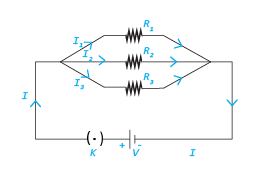 In parallel combination one end of each resistor is connected
with positive terminal of the battery while the other end of
each resistor is connected with the negative terminal of the
battery.
Therefore, the voltage is same across each resistor which is equal to the voltage of the battery i.e.,
V = V1 = V2 = V3
In parallel combination one end of each resistor is connected
with positive terminal of the battery while the other end of
each resistor is connected with the negative terminal of the
battery.
Therefore, the voltage is same across each resistor which is equal to the voltage of the battery i.e.,
V = V1 = V2 = V3
Equivalent Resistance of Parallel Circuit
In parallel circuit, the total current is equal the sum of the currents in various resistances i.e.,
$$ I = I_{1} + I_{2} + I_{3} \;\;\;\; \cdot \cdot \cdot \cdot (1)$$
Since the voltage across each resistance is V, so by Ohm's law
$$I_{1}= \frac{V}{R_{1}} $$
$$I_{2}= \frac{V}{R_{2}} $$
$$ I_{3}= \frac{V}{R_{3}} $$
$$ I= \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}} $$
$$ I= V (\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} ) $$
We can replace the combination of resistors with a single resistor called the equivalent resistance Re such that the same current passes through the circuit. From Ohm's law
$$I =\frac{V}{ R_{e}} $$.
Thus, Eq. 1 becomes
$$\frac{V}{R_{e}}= V (\frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} )$$
$$ \frac{1}{R_{e}}= \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} $$
Thus, the reciprocal of equivalent resistance of a parallel combination is sum of the reciprocals of the individual resistances, which is less than the smallest resistance of the combination.
If resistances R1, R2, R3, . . . . . . Rn are connected in parallel, then the equivalent resistance of the combination will be given by
$$ \frac{1}{R_{e}}= \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \cdot , \cdot , \cdot , \cdot + \frac{1}{R_{n}} $$
Parallel circuits have two big advantages over series circuits.
1. Each device in the circuit receives the full battery voltage.
2. Each device in the circuit may be turned off independently without stopping the current flowing to the other devices in the circuit. This principle is used in household wiring.
 In parallel combination one end of each resistor is connected
with positive terminal of the battery while the other end of
each resistor is connected with the negative terminal of the
battery.
Therefore, the voltage is same across each resistor which is equal to the voltage of the battery i.e.,
V = V1 = V2 = V3
In parallel combination one end of each resistor is connected
with positive terminal of the battery while the other end of
each resistor is connected with the negative terminal of the
battery.
Therefore, the voltage is same across each resistor which is equal to the voltage of the battery i.e.,
V = V1 = V2 = V3