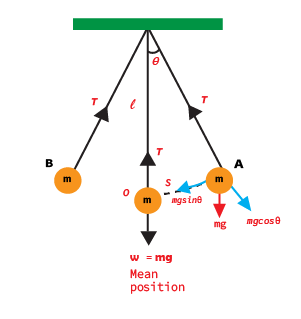
A simple pendulum also exhibits SHM. It consists of a small bob of mass ‘m’ suspended from a light string of length ‘ l ’ fixed at its upper end. In the equilibrium position O, the net force on the bob is zero and the bob is stationary.
A simple pendulum also exhibits SHM. It consists of a small bob of mass ‘m’ suspended from a light string of length ‘ l ’ fixed at its upper end. In the equilibrium position O, the net force on the bob is zero and the bob is stationary.
Now if we bring the bob to extreme position A, the net force is not zero. The component of weight \(mg cos\theta\) is in opposite direction to tension T in the string so they cancel each other. Hence there is no motion along this direction.
The component of the weight \(mg sin\theta\) is directed towards the mean position and acts as a restoring force. Due to this force the bob starts moving towards the mean position O. At O, the bob has got the maximum velocity and due to inertia, it does not stop at O rather it continues to move towards the extreme position B. During its motion towards point B, the velocity of the bob decreases due to restoring force. The velocity of the bob becomes zero as it reaches the point B.
The restoring force \(mg sin\theta\) still acts towards the mean position O and due to this force the bob again starts moving towards the mean position O. In this way, the bob continues its to and fro motion about the mean position O.
It is clear from the above discussion that the speed of the bob increases while moving from point A to O due to the restoring force which acts towards O. Therefore, acceleration of thebob is also directed towards O. Similarly, when the bob moves from O to B, its speed decreases due to restoring force which again acts towards O. Therefore, acceleration of the bob is again directed towards O. It follows that the acceleration of the bob is always directed towards the mean position O. Hence the motion of a simple pendulum is SHM.
We have the following formula for the time period of a simple pendulum $$ T= 2 \pi \sqrt{\frac{l}{g}} $$
Let the bob of pendulum of mass m having weight w is displaced from mean position ‘O’ towards A. Weight w acts vertically in downward direction, ‘l’ is length of pendulum which is the sum of the length of string plus the radius r of the metallic bob. T is the tension in string.
Now resolve w into its components.
$$T= mg cos\theta $$
T and \(mg cos\theta\) balance each other .
Now the component of weight that is acting towards the mean position is \(mg sin\theta\). This component is responsible for pendulums motion towards mean position so net met force on pendulum is $$F_{net}= -mgsin\theta $$ $$ma = -mgsin\theta$$ $$a =-gsin\theta \;\;\;\;\; \cdot \cdot \cdot \cdot (1)$$ if θ is very small $$sin\theta \widetilde{-} \theta$$ so $$a=-g\theta$$ But when θ is very small, point O will be very near to point A and arc OA=x is a straight line then ΔAOC will be a right angle triangle. $$So \;\;\;\; \frac{x}{l} = sin\theta = \theta$$ then eq 1 becomes $$a=-g \frac{x}{l}$$ $$a=- \frac{g}{l}x \;\;\;\; \cdot \cdot \cdot \cdot (2)$$ as g and l are constant so $$a = – constant \times x$$ $$a \propto -x$$ This is equation of SHM so motion of pendulum is SHM.
From above eq 2 $$a=- \frac{g}{l}x $$ we know for the motion of projection of body moving in circle that $$a=-\omega^2 x$$ By comparing both equations $$\omega^2 = \frac{g}{l}$$ $$\omega = \sqrt{\frac{g}{l}}$$ By definition $$T= \frac{2\pi}{\omega}$$ $$so \;\;\;\; T= \frac{2\pi}{\sqrt{\frac{g}{l}}}$$ $$so \;\;\;\; T= 2\pi \sqrt{\frac{l}{g}}$$