Projectile Motion:

Projectile motion is two dimensional motion under constant acceleration due to gravity. Such moving body is called projectile.

Case1:

Consider the motion of ball when it is thrown horizontally from certain height. It is observed that the ball travels forward as well as falls downwards, until it strikes something. Suppose that the ball leaves the hand of thrower at point A and its velocity at that time is completely horizontal. Let this velocity be v_x. According to Newton’s first law of motion, there will be no acceleration along x-axis. So v_x will not change. Hence horizontal distance x can be calculated as $$ x= v_{x} \times t $$ The only force acting on the ball is the force of gravity. So velocity it accelerate downward under the force of gravity and hence a = g . This vertical motion is same as for a freely falling body. Since initial velocity along y-axis v_iy is zero so we can calculate vertical distance y as $$ y=v_{iy} t + \frac{1}{2}gt^{2} $$ $$ y= (0) t + \frac{1}{2}gt^{2} $$ $$ y= \frac{1}{2}gt^{2} $$

Case 2:

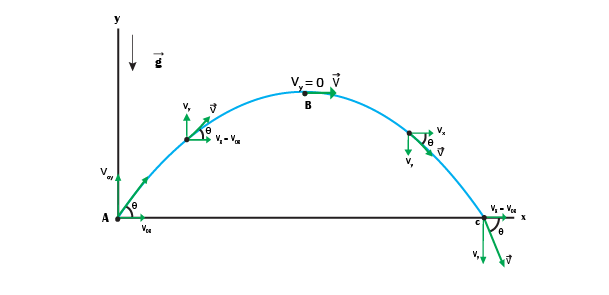
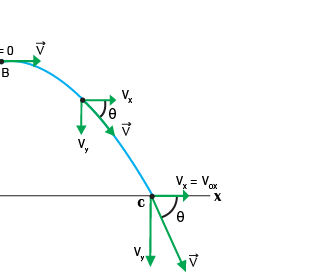
Let an object is thrown in air with initial velocity v_i and angle θ with x-axis. The object will move upwards as well as forward. This means it is covering distance along Y-axis and also along X-axis. As it moving upward its velocity will decrease due to force of gravity. At highest point its velocity along y-axis will become zero and then it will start moving downward with acceleration g.

In this case the motion of projectile can be studied easily by resolving it into horizontal and vertical components which are independent of each other. Let components of velocity v_i along x-axis is given by $$v_{ix}= v_{i}cos\theta $$ As air resistance is neglected and there is no acceleration along x-ais therefore $$ v_{fx}= v_{ix}+at $$ $$ v_{fx}= v_{ix}+(0)t $$ $$ v_{fx}= v_{ix} $$ So velocity along x-axis will remain constant i.e $$ v_{fx}= v_{ix} = v_{i}cos\theta $$ Now consider the motion along y-axis. The initial velocity component along y-axis is $$ v_{iy}= v_{i}sin\theta $$ Final velocity along y-axis v_fy is given by $$ v_{fy}= v_{iy}+at $$ since body is moving upward a= -g $$ v_{fy}= v_{i}sin\theta -gt $$ The magnitude of resultant velocity at any instance is $$ v= \sqrt{v^{2}_{fx}+v^{2}_{fy}} $$ The angle ϕ of resultant velocity is $$ tan\phi = \frac{v_{fy}}{v_{fx}} $$

Maximum Height of Projectile:

To calculate maximum height of projectile we use the equations $$ 2aS= v^2_{fy} – v^2_{iy} $$ As body moves upward $$ a=-g $$ $$ v_{iy}= v_{i}sin\theta $$ $$ v_{fy}= 0 \because \; at \;highest \;point \;y-velocity \; will \; be \;zero $$ $$ S=height=h $$ $$ So $$ $$ -2gh= 0 – v^2_{i}sin^2\theta $$ $$ h=\frac{v^2_{i}sin^2\theta}{2g} $$ $$ $$

Time of Flight:

The time taken by the body to cover the distance from the place o its projection to the place where it hits the ground at the same level is called the time of flight.

As body goes up and comes down to hit the ground so at the time of its vertical distance is zero. So we use the equation $$ S = v_{i}t + \frac{1}{2}g t^2 $$ $$ For \;Y-axis $$ $$ 0 = v_{iy}t- \frac{1}{2}g t^2 $$ $$ 0= v_{i}sin\theta t - \frac{1}{2}g t^2 $$ $$ \frac{1}{2}g t^2 = v_{i}sin\theta t $$ $$ \frac{1}{2}g t = v_{i}sin\theta $$ $$ t = \frac{2v_{i}sin\theta }{g} $$

Range of Projectile:

Maximum distance which a projectile covers in horizontal direction (along X-axis) is called the range of the projectile.

To determine the range R of the projectile we use the equation $$ S= vt $$ here we will use the x-component of v_i and time is the total time of flight of projectile So $$ R=v_{ix}\times t $$ $$ R= \frac{v_{i}cos\theta \times 2v_{i}sin\theta}{g} $$ $$ R= \frac{v^2_{i}}{g} 2 sin\theta cos\theta $$ $$ But $$ $$ 2 sin\theta cos\theta = sin2\theta $$ $$ So $$ $$ R= \frac{v^2_{i}}{g} sin2\theta $$

Trajectory of Projectile:

The path followed by a projectile is called its trajectory. The trajectory can be calculated using formula $$ y= x tan\theta - \frac{g}{2v^2_{i} cos^2\theta}x^2 $$ This is equation of parabola so trajectory of projectile is parabola