Moment of Inertia

A tendency of a body to resist any change in its state of rest or rotational motion is called moment of inertia or rotational inertia.

It depends upon mass and the distance between axis of rotation and centre of mass of the body.

Greater is the moment of inertia, the greater is torque required to rotate or stop the body about an axis of rotation. Thus by definition of torque $$ \overrightarrow{\tau} = \overrightarrow{r} \times \overrightarrow{F} $$ As the ‘θ’ between r and F is 90 $$ \tau = r F sin90 $$ $$ \tau = r F \;\;\;\; \cdot \cdot \cdot \cdot (1) $$ According to Newton’s 2^nd law $$ F=ma $$ putting value of F in eq (1) $$ \tau = rma $$ As $$ a=r \alpha $$ $$ \tau = rm(r \alpha)$$ $$ \tau=mr^2\alpha$$ This equation shows that torque is proportional to angular acceleration while mr² is constant and is known as moment of inertia of the body. It is represented by I so $$ I=mr^2$$ This equation can be used to calculate the moment of inertia of a rigid body which has regular geometrical shape.

The SI unit of moment of inertia is kg m². Its dimensional formula is [ML²T⁰]

Rotational Kinetic Energy

The energy possessed by a body due to rotational motion is called rotational kinetic energy

By definition of translational K.E. $$ K.E = \frac{1}{2}mv^2 $$ But $$ v=r\omega$$ $$ K.E = \frac{1}{2}mr^2\omega^2 $$ $$ K.E = \frac{1}{2}I\omega ^2 $$ This is the rotational K.E of the body in terms of moment of inertia

Rolling of sphere at an inclined plane

Consider a sphere of mass ‘m’ which is rolling down on an inclined plane. The inclined plane is making an angle of θ with horizontal plane. Its lower end is at ground level while other is at a height h from the ground.

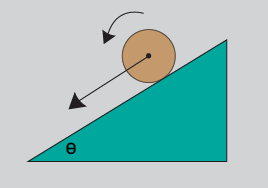
When it starts rolling, it gain both translational and rotational kinetic energies due to increase in its velocity. As it is moving downward, its potential energy is decreasing.